Download the notebook here!
Interactive online version:
Uncertainty propagation¶
We show how to conduct uncertainty propagation for the EOQ model. We can simply import the core function from temfpy.
[1]:
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
import chaospy as cp
from temfpy.uncertainty_quantification import eoq_model
from econsa.correlation import gc_correlation
Setup¶
We specify a uniform distribution centered around \(\mathbf{x^0}=(M, C, S) = (1230, 0.0135, 2.15)\) and spread the support 10% above and below the center.
[2]:
marginals = list()
for center in [1230, 0.0135, 2.15]:
lower, upper = 0.9 * center, 1.1 * center
marginals.append(cp.Uniform(lower, upper))
Independent parameters¶
We now construct a joint distribution for the the independent input parameters and draw a sample of \(1,000\) random samples.
[3]:
distribution = cp.J(*marginals)
sample = distribution.sample(10000, rule="random")
The briefly inspect the joint distribution of \(M\) and \(C\).
[5]:
plot_joint(sample)

We are now ready to compute the optimal economic order quantity for each draw.
[6]:
y = eoq_model(sample)
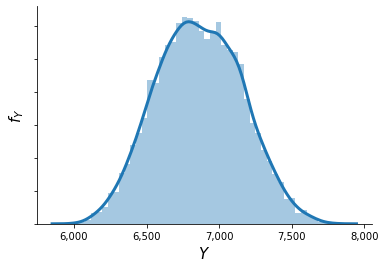
This results in the following distribution \(f_{Y}\).
[8]:
plot_quantity(y)
Depdendent paramters¶
We now consider dependent parameters with the following correlation matrix.
[9]:
corr = [[1.0, 0.6, 0.2], [0.6, 1.0, 0.0], [0.2, 0.0, 1.0]]
We approximate their joint distribution using a Gaussian copula. This requires us to map the correlation matrix of the parameters to the correlation matrix of the copula.
[10]:
corr_copula = gc_correlation(marginals, corr)
copula = cp.Nataf(distribution, corr)
We are ready to sample from the distribution.
[11]:
sample = copula.sample(10000, rule="random")
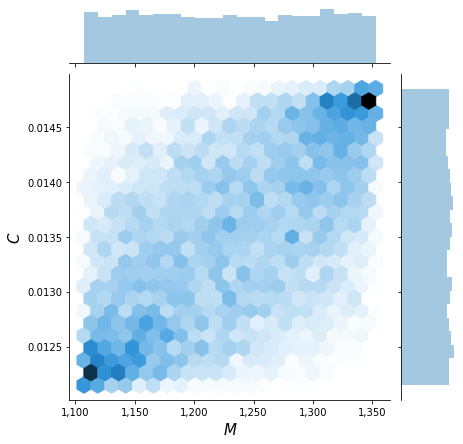
Again, we briefly inspect the joint distribution which now clearly shows a dependence pattern.
[12]:
plot_joint(sample)
[13]:
y = eoq_model(sample)
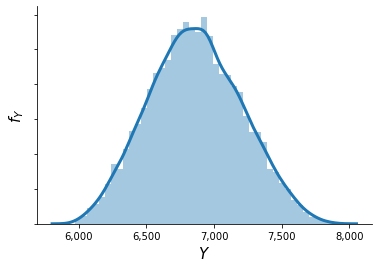
This now results in a distribution of \(f_{Y}\) where the peak is flattened out.
[14]:
plot_quantity(y)